State of the System: A real number x.
Rule of Evolution: 
, where a and b are parameters
which we can fixed at our will but which stay constant during the evolution.
Motivations:
Given a well-behaved function g, a point y
and a sufficiently small value of x,
we have 
where a and b
can be calculated with the help of
calculus (it is called a Taylor expansion). In other words, at
a sufficiently small scale, a curve looks like straight line.
``Real Life'' Example:
A simple application of the linear map is the following. Let us
call 
the amount of money deposited in a bank at a given time,
the amount of money on the account a year after,
the amount of money on the account two years after, etc...
To calculate , 
, we assume that an interest of 5 percent
is added every year, that the bank gives a fixed amount (say 1 dollar)
every year to its customers and that no additional money is deposited.
The evolution rule is then 
.
Main Result:
If 
, the system has a fixed point 
such that
if 
, then 
.
We can discuss the evolution using either graphical methods (see
``graphical representation .. `` below) or by algebraic methods.
If we write 
, 
, etc. , then
a little algebra shows that
. It is easy to study the series 
.
If b<0, the signs altenate otherwise the series is the same as for |b|.
If |b|<1 then 
becomes smaller and smaller when n increases and
tends to its fixed point value. Such a fixed point is called
attractive.
if |b|>1 then becomes larger and larger, and moves
away from the fixed point. Such a fixed point is
called repulsive.
When the fixed point is repulsive, if you start on the right of
the fixed point you move farther right when n increases.
But if you start on the left of
the fixed point, you move farther left.
If b=1, then 
and goes to
infinity but at a slower rate than when |b|>1
(linear rather than exponential).
If b=-1, 
, 
and we are back at our
starting point after two steps. We call this particular type of periodic
behavior a 2-cycle.
Important Concepts: Attractive and repulsive fixed point, 2-cycle.
Graphical Representations and Examples
It is often convenient to represent graphically the series 
.
For this purpose we draw the function used for the map (here a+bx).
The graph of the function a+bx is a straight line, so we only need
two points to draw it. For instance at x=0, the value of the function
is a and for x=1, the value of the function is a+b.
We then
pick on the x-axis, go vertically
to the function, in other words,
we will be at the point 
. We would like to repeat the procedure
with . In order to do that, we need to move on the x-axis
and so we move horizontally to the x=y line and we arrive
at the 
point. We have now on the x-axis, we move vertically
to the function and arrive at the point 
and so on.
This procedure is illustrated in examples which illustrate the
six cases dicussed above.
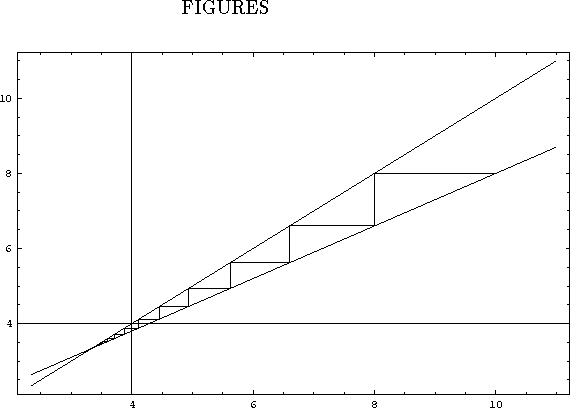
Figure: 10 Iterations of the linear map with a=1, b=0.7 and 
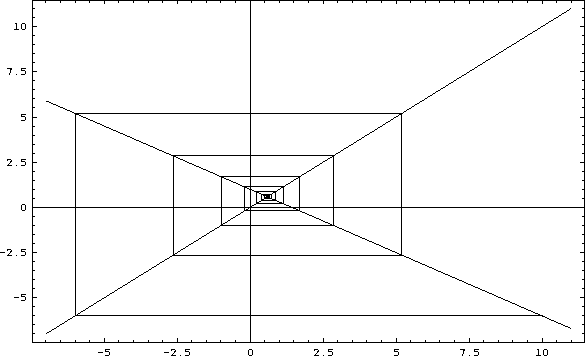
Figure: 10 Iterations of the linear map with a=1, b=-0.7 and
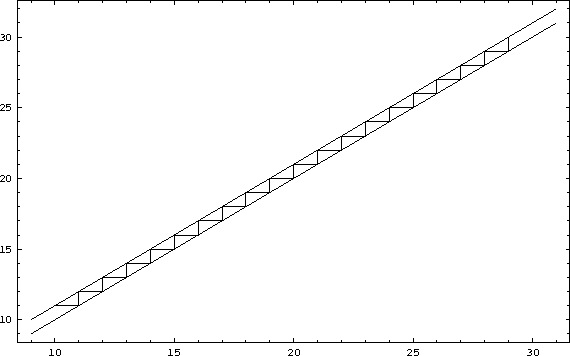
Figure: 10 Iterations of the linear map with a=1, b=1 and
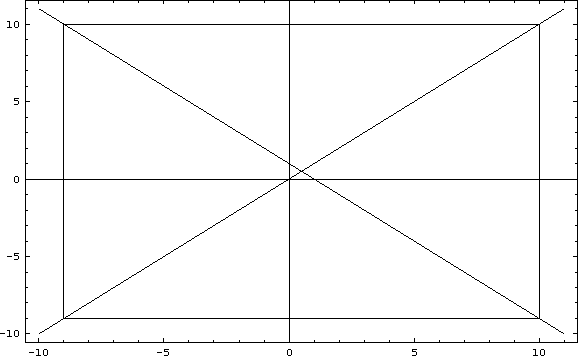
Figure: 10 Iterations of the linear map with a=1, b=-1 and
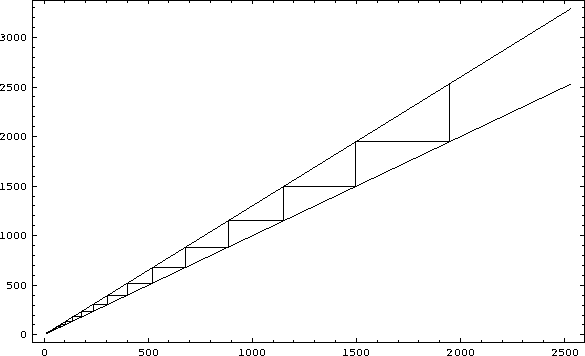
Figure: 10 Iterations of the linear map with a=1, b=1.3 and
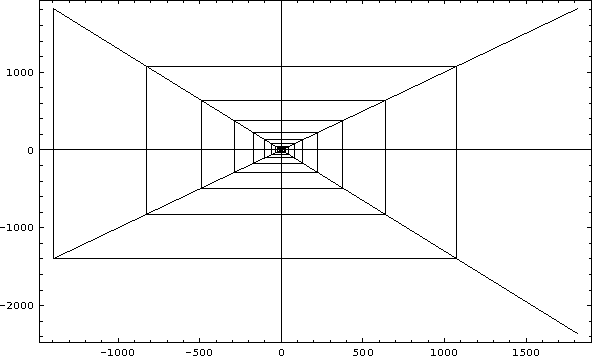
Figure: 10 Iterations of the linear map with a=1, b=-1.3 and