

where 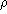 = (average n)/V
is the constant density mentioned above. It is
clear that if the density is not constant, for example if the raisins
have settled to the bottom, this equation will not be sufficient to
describe the probability of finding n raisins in a given volume.
= (average n)/V
is the constant density mentioned above. It is
clear that if the density is not constant, for example if the raisins
have settled to the bottom, this equation will not be sufficient to
describe the probability of finding n raisins in a given volume.
In the case of a counting experiment, if the average count rate (average
number of counts per unit time, or count density) is
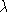 , the probability
of observing n counts in time t is
, the probability
of observing n counts in time t is

Many other examples can be given (number of stars per unit volume of space, number of V2 rocket explosions per square block in London during WW2, etc.) but Eq. (6) is the one applicable to this experiment.

Examples are such everyday occurrences as flipping a coin (p = 1/2 if the coin is unbiased) or the tossing of a die (p = 1/6 if the die is not loaded).
The condition that the results of a physical measurement be distributed according to a normal distribution are very general indeed. To illustrate this generality we give a non-rigorous statement of what is called the central limit theorem of statistics: If the result of some measurement depends on the combined effect of many random causes it will be distributed according to a normal distribution provided only that none of the causes contribute too much to the effect and that each of the causes be distributed according to distributions that have finite means and variances. Mathematically the normal distribution is the continuous limit of the binomial distribution, the limit being such that N goes to infinity, n goes to infinity, with n/N and np remaining finite. incidentally, the Poisson distribution is also a limiting form of the binomial distribution, the limit in this case being such that p goes to 0, n goes to infinity with np remaining finite. It is rewarding to reflect at length on the connection between the three distributions given above.
The form of the normal distribution is
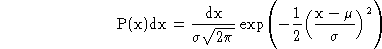
where µ is the mean value of x and sigma is the standard deviation.
Given the forms of the distributions, the means and standard deviations may be calculated directly from the defining equations (3) and (4). The results are summarized below. .b2 .ts 2,18,51,60 !!Form!Mean!Deviation[[\\\\\\\\\Standard]] .b !Poisson!P]t[(n) = (<)[n] {e[-<]}/{n@!}!<!&R<[[[\\@_@_]]] .b2 !Binomial!P]N[(n) = {N@!}/{n@!(N-n)@!}p[n](1-p)[N-n]!np!&Rnp(1-p)\\\\\\\[[[~ @_@_@_@_@_@_@_]]] .b2 !Normal!P(x)dx = {dx}/{&s&R2&p}exp&[-{1}/{2}({x-&m}/{&s})[&2]&]!&m!&s