1. For a transverse wave on a string the string displacement is described by y(x,t) = f(x–at) where f is a given function and a is a positive constant. Which of the following does NOT necessarily follow from this statement?
A.The shape of the string at time t = 0 is given by f(x).
B.The shape of the waveform does not change as it moves along the string.
C.The waveform moves in the positive x direction.
D.The speed of the waveform is a.
E.The speed of the waveform is x/t.


2.

A sinusoidal wave is traveling toward the right as shown. Which letter correctly labels the amplitude of the wave?




A.A
B.B
C.C
D.D
E.E


3. Let f be the frequency, v the speed, and T the period of a sinusoidal traveling wave. The correct relationship is:
A.f = 1/T
B.f = v + T
C.f = vT
D.f = v/T
E.f = T/v


4.

The displacement of a string is given by


y(x,t) = ymsin(kx + wt).


The wavelength of the wave is:


A.2pk/w
B.k/w
C.wk
D.2p/k
E.k/2p


5.

Three traveling sinusoidal waves are on identical strings, with the same tension. The mathematical forms of the waves are y1(x,t) = ymsin(3x – 6t), y2(x,t) = ymsin(4x – 8t), and y3(x,t) = ymsin(6x – 12t), where x is in meters and t is in seconds. Match each mathematical form to the appropriate graph below.




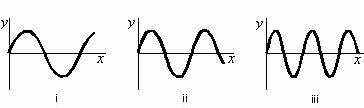
A.y1: i, y2: ii, y3: iii
B.y1: iii, y2: ii, y3: i
C.y1:i, y2: iii, y3: ii
D.y1: ii, y2: i, y3: iii
E.y1: iii, y2: i, y3: ii


6. A wave is described by y(x,t) = 0.1 sin(3x + 10t), where x is in meters, y is in centimeters and t is in seconds. The wavelength is:
A.6p m
B.3p m
C.2p/3 m
D.p/3 m
E.0.1 cm


7. Water waves in the sea are observed to have a wavelength of 300 m and a frequency of 0.07 Hz. The velocity of these waves is:
A.0.00021 m/s
B.2.1 m/s
C.21 m/s
D.210 m/s
E.none of these


8.

The displacement of a string carrying a traveling sinusoidal wave is given by


y(x,t) = ymsin(kx – wt – f ).


At time t = 0 the point at x = 0 has velocity v0 and displacement y0. The phase constant f is given by tanf =:


A.v0/wy0
B.wy0/v0
C.wv0/y0
D.y0/wv0
E.wv0y0


9. A sinusoidal transverse wave is traveling on a string. Any point on the string:
A.moves in the same direction as the wave
B.moves in simple harmonic motion with a different frequency than that of the wave
C.moves in simple harmonic motion with the same angular frequency as the wave
D.moves in uniform circular motion with a different angular speed than the wave
E.moves in uniform circular motion with the same angular speed as the wave


10.

The transverse wave shown is traveling from left to right in a medium. The direction of the instantaneous velocity of the medium at point P is:




A.­
B.¯
C.®
D.«
E.no direction since v = 0


11. Sinusoidal waves travel on five identical strings. Four of the strings have the same tension, but the fifth has a different tension. Use the mathematical forms of the waves, gives below, to identify the string with the different tension. In the expressions given below x and y are in centimeters and t is in seconds.
A.y(x,t) = (2 cm) sin (2x – 4t)
B.y(x,t) = (2 cm) sin (4x – 10t)
C.y(x,t) = (2 cm) sin (6x – 12t)
D.y(x,t) = (2 cm) sin (8x – 16t)
E.y(x,t) = (2 cm) sin (10x – 20t)


12. Any point on a string carrying a sinusoidal wave is moving with its maximum speed when:
A.the magnitude of its acceleration is a maximum
B.the magnitude of its displacement is a maximum
C.the magnitude of its displacement is a minimum
D.the magnitude of its displacement is half the amplitude
E.the magnitude of its displacement is one fourth the amplitude


13. Suppose the maximum speed of a string carrying a sinusoidal wave is vs. When the displacement of a point on the string is half its maximum, the speed of the point is:
A.vs/2
B.2vs
C.vs/4
D.3vs/4
E.


14. A transverse traveling sinusoidal wave on a string has a frequency of 100 Hz, a wavelength of 0.040 m and an amplitude of 2.0 mm. The maximum acceleration in m/s2 of any point on the string is:
A.0
B.130
C.395
D.790
E.1600


15. The speed of a sinusoidal wave on a string depends on:
A.the frequency of the wave
B.the wavelength of the wave
C.the length of the string
D.the tension in the string
E.the amplitude of the wave


16. The time required for a small pulse to travel from A to B on a stretched cord shown is NOT altered by changing:
A.the linear density of the cord
B.the length between A and B
C.the shape of the pulse
D.the tension in the cord
E.none of the above (changes in all alter the time)


17.

The diagram shows three identical strings that have been put under tension by suspending masses of 5 kg each. For which is the wave speed the greatest?




A.1
B.2
C.3
D.1 and 3 tie
E.2 and 3 tie


18. An oscillatory motion must be simple harmonic if:
A.the amplitude is small
B.the potential energy is equal to the kinetic energy
C.the motion is along the arc of a circle
D.the acceleration varies sinusoidally with time
E.the derivative, dU/dx, of the potential energy is negative


19. An object is undergoing simple harmonic motion. Throughout a complete cycle it:
A.has constant speed
B.has varying amplitude
C.has varying period
D.has varying acceleration
E.has varying mass


20. When a body executes simple harmonic motion, its acceleration at the ends of its path must be:
A.zero
B.less than g
C.more than g
D.suddenly changing in sign
E.none of these


21. Two identical undamped oscillators have the same amplitude of oscillation only if:
A.they are started with the same displacement x0
B.they are started with the same velocity v0
C.they are started with the same phase
D.
E.


22. It is impossible for two particles, each executing simple harmonic motion, to remain in phase with each other if they have different:
A.masses
B.periods
C.amplitudes
D.spring constants
E.kinetic energies


23. The acceleration of a body executing simple harmonic motion leads the velocity by what phase?
A.0
B.p/8 rad
C.p/4 rad
D.p/2 rad
E.p rad


24. The displacement of a mass oscillating on a spring is given by x(t) = xmcos(w t + f ). If the initial displacement is zero and the initial velocity is in the negative x direction, then the phase constant f is:
A.0
B.p/2 radians
C.p radians
D.3p/2 radians
E.2p radians


25. A particle is in simple harmonic motion along the x axis. The amplitude of the motion is xm. At one point in its motion its kinetic energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is U = 3J. When it is at x = xm, the kinetic and potential energies are:
A.K = 5J and U = 3J
B.K = 5J and U = –3J
C.K = 8J and U = 0
D.K = 0 and U = 8J
E.K = 0 and U = –8J


26. The period of a simple pendulum is 1 s on Earth. When brought to a planet where g is one-tenth that on Earth, its period becomes:
A.1 s
B.
C.1/10 s
D.
E.10 s


27. A simple pendulum consists of a small ball tied to a string and set in oscillation. As the pendulum swings the tension in the string is:
A.constant
B.a sinusoidal function of time
C.the square of a sinusoidal function of time
D.the reciprocal of a sinusoidal function of time
E.none of the above


28. A simple pendulum is suspended from the ceiling of an elevator. The elevator is accelerating upwards with acceleration a. The period of this pendulum, in terms of its length L, g and a is:
A.
B.
C.
D.
E.


29.

Below are sets of values for the spring constant k, damping constant b, and mass m for a particle in damped harmonic motion. Which of the sets takes the longest time for its mechanical energy to decrease to one-fourth of its initial value?


k

b

m


A.


k0

b0

m0


B.


3k0

2b0

m0


C.


k0/2

6b0

2m0


D.


4k0

b0

2m0


E.


k0

b0

10m0




30.

A sinusoidal wave is traveling toward the right as shown. Which letter correctly labels the wavelength of the wave?




A.A
B.B
C.C
D.D
E.E



This is the end of the test. When you have completed all the questions and reviewed your answers, press the button below to grade the test.