If a penny is tossed with a good amount of spin, it is hopeless to predict on which side it will land. We denote the two possible outcomes of the experiment H (for head) and T (for tail). If we repeat the experiment a (large) number N of times, we obtain N(T) tails and N(H) heads. The fraction N(H)/N can be interpreted as the ``chance'' to get a head. If the coin is symmetrical and if N is large, we expect N(H)/N to be close to 0.5. The mathematical name for chance is probability. We call P(T) the probability to get a tail and P(H) the probability to get a head. A probability is a number between 0 and 1. If we associate a probability 1 with a given event, it means that this event will occur with certainty. On the other hand, a probability 0 means an impossibility. If two events A and B are incompatible, then the probability to have A or B is the sum of the probability to have A and the probability to have B. In our example of tossing a coin once, we get either a head or a tail but never both at the same time, this implies that
![]()
For a symmetrical coin P(H)=P(T)=0.5.
We can repeat the toss twice. The four possible outcomes will be: HH, HT, TH and TT. The two tosses are independent. It means that result of the first toss does not influence the second toss. Consequently we just have to multiply the probability for the two individual events in order to get the probability of the combined events. For instance, P(HT)=P(H)P(T). We can then write
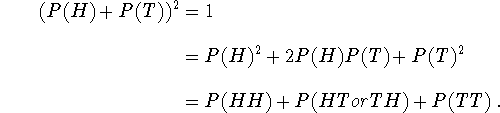
In other words,
![]() ,
,
![]() and
and
![]() .
.
This method can be extended to m tosses by using
where m! means ![]() .
.
Proceeding as in the case of two tosses, we obtain
The references for this subsection are Feynman's Lectures vol.1 chapter 6 sections 1 to 3, and chapters 3 and 4 of Ruelle's book Chance and Chaos.
Exercise : A coin is tossed 30 times. We assume the the coin
is symmetrical under the exchange of head and tail and that the probabilities
to get head or tail are both equal to 1/2. Let n be the number of tails
obtained after the 30 tosses. What is the mean value of n?
What is the probability to get n=15 exactly? What is the probability
that ![]() ? What is the probability
that
? What is the probability
that ![]() ?
?