Another example of irregular sequence of numbers are the so-called ``random number generators'' used in many sampling procedures. A simple algorithm is given by the (deterministic) rule
for judiciously chosen values of a and m.
A very popular choice due to Lewis, Goodman and Miller is 
and
(see Press et al., Numerical Recipes, Chapter on
Random Numbers). Detailed studies (way beyond the scope of this course)
show that with this choice,
the distribution of numbers is reasonably uniform and
successive sequences of numbers of a given length are
reasonably independent.
In order to get numbers between 0 and 1, we take
the value of 
between 0 and m and then we divide it by m.
We now proceed to study the distribution of values of the numbers
obtained with this procedure.
We first divide the interval [0,1] into 100 bins of width 0.01.
We then compare the distributions for one thousand, ten thousands and hundred
thousands values of . In order to be able to compare these three
distributions, we do not display the absolute number of visits in each
bin, but rather this number divided by the total number of visits.
This gives the fraction of visits in each bins. If the distribution was
perfectly uniform, one would get a fraction 0.01 in each of the hundred bins.
Using 1,000 numbers we see in Figure /reffig:hl0 that this
situation is far from realized.
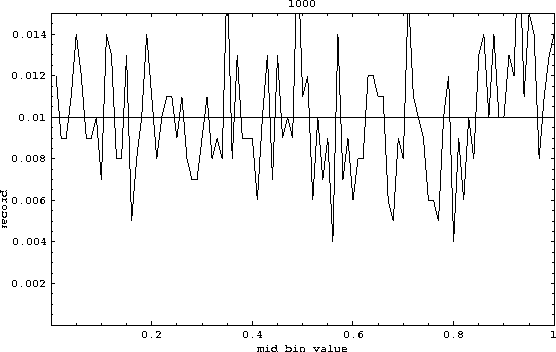
Figure 4: Fraction of visits in bins of size 0.01 for 1,000 numbers
However as seen in Figs.5 and 6, we obtain a more uniform distributions by increasing the number of points.
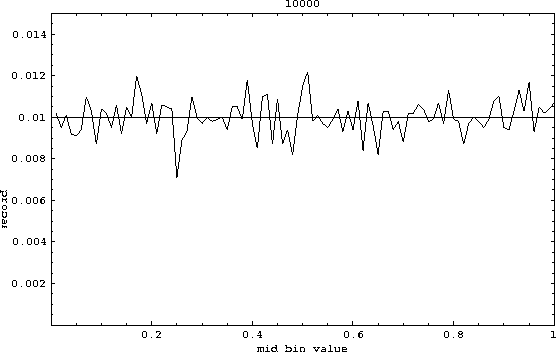
Figure 5: Fraction of visits in bins of size 0.01 for 10,000 numbers .
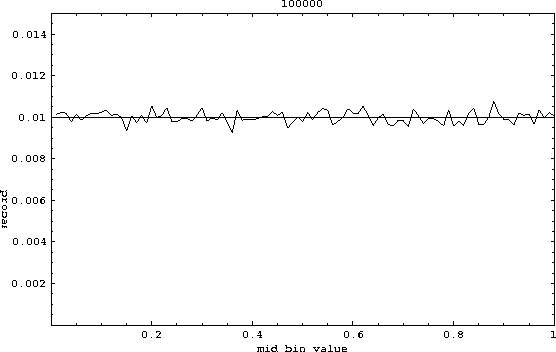
Figure 6: Fraction of visits in bins of size 0.01 for 100,000 numbers .
The rule of the thumb with the fluctuations (departures from uniformity
in this case) is that if we expect N visit in a bin, variations of
order 
are not uncommon. For instance in Figure 4,
we expect 1000/100=10 visits in each bin from uniformity. The rule of the
thumb tells us that bins with 7 or 13 visits (in other words,
fractions of visits 0.07 or 0.013) will not be uncommon. In
Figure 6, we have 100,000 points which would visit each bins
1,000 times for a uniform distribution. Since 
, bins
with fractions such as 0.0103 or 0.0097 are not uncommon.
In the following, we will use this random number generator as a way to
simulate coin tossing.