We shall now discuss some general features of dynamical systems which evolve continuously in time (as in Example 3 in section 1) from their initial conditions according to deterministic laws. We remind that by deterministic laws, we mean rules which allow to predict uniquely and unambiguously the evolution given the initial state. The discussion which follows is a simplified version of the Chapter 1 of the book Ordinary Differential Equations by V.I. Arnold.
We assume that the laws of evolution are deterministic and
that the state of the system can be completely specified by fixing the
values of a finite
number of variables.
The set of all the possible values is called 
.
Given the state of the system at some initial time,
the evolution can then be described by a curve emerging from the
point associated with the initial state. Such a curve is called a 
.
If the law of evolution are deterministic, two phase curves
cannot ``cross'' each other or more precisely cannot
intersect without either stopping their evolution at the
point of intersection or retracing exactly their path.
This simple observation has far reaching
consequences if we try to use empirical
observations to draw the phase curves representing the evolution
of a physical (or chemical, or biological etc..) system.
In that case, we do not know a-priori what is the .
Consequently, if we observe phase curves intersecting each other or themselves without stopping as in the figure below
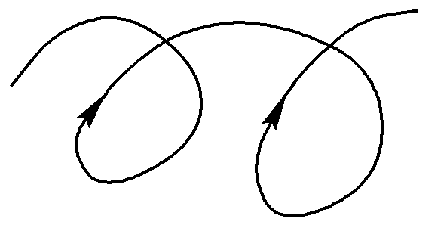
Figure 1: Example of a self-intersecting path in two dimensions.
we know that additional variables are necessary for a deterministic interpretation. Otherwise, if the point of intersection is taken as the initial state, we would have to decide between two distinct evolutions, a situation which does not occur for deterministic rules of evolution. If additional variables are appropriately chosen, it is possible to make the previously observed intersections disappear. You can use your imagination to ``pull'' the curve in a third dimnsion in such a way that it does not intersect with itself anymore.
On the other hand, the phase curves of a deterministic system
may intersect at a 
(also called equilibrium point).
As in other examples discussed in section 1, the fixed points are
characterized by an absence of evolution. If the state of the system
is given by a point close to a fixed point, it is interesting to see
if this state is ``attracted'' or ``repelled'' by the fixed point.
A fixed point which is completely attractive is called a stable fixed
point.
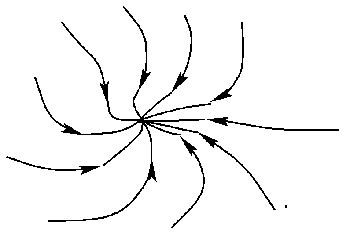
Figure 2: Example of an attractive fixed point in two dimensions.
A fixed point which is completely repulsive is called an unstable fixed point. An example can be obtained by reversing the directions of the arrows of the phase curves of an attractive fixed point.
Mixed cases are also possible.
Figure 3: Example of a ``mixed'' fixed point.
Note that a phase curve can retrace its path and form a cycle.
Figure 4: Example of a self-intersecting path in two dimensions.
This is also compatible with a deterministic evolution because we never have to choose between two alternative directions as in the example shown above.