The set of all the possible phase curves is often called the 
,
in analogy with the motion of a fluid visualized as the motion of many small
particles flowing beside each others. Let suppose that we have a reasonably
good knowledge of the phase flow, can we derive the laws that determine
the shape of the phase curves? The answer to this question is yes and
the laws of evolution are called ordinary differential equations
(ODE for short).
In order to explain this statement, let us discuss it in the special
case where the state of the system is specified by two variables x
and y,
and the where the phase curves
can be drawn on a flat sheet of paper.
If at time 0, the state of the system is given by (x(0),y(0)),
then the state of the system at time t,
is given by two functions of t and the initial state
(g(t,(x(0),y(0))),h(t,(x(0),y(0)))) which we
assume can be obtained by empirical
observations. In each point of the curve,
we can draw a 
which indicates the direction the curve
would follow if it were suddenly following a straight trajectory.
Figure 5: Example of vector tangent to a curve in two dimensions.
More precisely, the tangent vector at the point of the curve characterizing
the state of the system at time t is defined as
, where
is defined by the following limit (called the time derivative):
and 
is defined similarly.
We can now forget about the curves and just keep the tangent vectors.
We denote the tangent vector at the point (x,y), (v(x,y),w(x,y)).
We use a different notations than ( 
to emphasize that v and w are now given
and that we have to derive the phase curves.
If (x(t),y(t)) is an unspecified curve parametrized by t, the tangent
vector to this curve can be calculated as above and will be denoted
.
The law of evolution consists in imposing the matching
between these tangent vectors and (v(x(t),y(t)),w(x(t),y(t))).
The general form of an ODE of two variables is
We can now follow the opposite route and show that the above equations
fix uniquely a curve emerging from the point representing the initial
state of the system. The pair (v(x,y),w(x,y)), determine at each point
(x,y) the direction followed by the curve during an arbitrarily
short instant,
while it passes through this point.
The change can be approximately calculated by taking finite time steps
of duration 
and replacing 
by 
and similarly for 
. Using the notations
and 
, we obtain after a little
algebra
By taking small, one can calculate a sequence of 
which follows approximately the phase curve emerging from 
.
Note that more precise numerical methods exist but a more
complicated discussion is necessary to justify them.
You can also get a qualitative description of the flow by drawing
(v(x,y),w(x,y)) at selected points.
More sophisticated methods can be used to solve or simplify ODE. For instance, if v(x,y) and w(x,y) are linear functions of x and y, i.e., if they can be written as ax+by with a and b constant, then one can find explicit solutions involving exponential or trigonometric functions. ODE can sometimes be solved (or simplified) by finding one or several constants of motion, i.e., quantities which do not change with time and keep their initial values. In each cases, basic calculus results are necessary. We give below a few useful formulas which can be derived from the expansion formula given above.
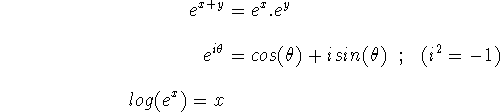
Exercise: study the phase curves for the following ordinary differential equations:
i)
hint: show that x/y is a constant of motion.
ii)
hint: show that xy is a constant of motion.
iii)
hint: show that 
is a constant of motion.