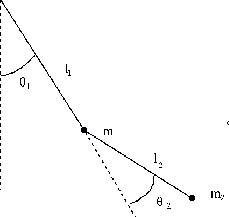
Figure 8: The double pendulum.
In the two examples considered above (oscillating spring and simple pendulum), all the phases curves (except the ones which ``separate'' the two types of behavior for the planar pendulum) return to their starting point after a finite amount of time. We call such a trajectories periodic. In both cases, the state of the system is described by two variables, and there exists one constant of motion (the energy) which ``forces'' the phase curves to close into themselves.
A more complex behavior is obtained for the double pendulum. The state of the system is described by four variables: two angles and two angular velocities.

Figure 8: The double pendulum.
If you want to see the exact form of the equations of motion, you can find them in the notebook related to the double pendulum. Numerical simulations have been shown in class (the tape can be obtained at the Physics Library). There is always one constant of motion (again the total energy). In the limits where the total energy is very small, the system can be described by two independent oscillators, the energy of each of them being a constant of motion. In the limit where the energy is very large, the effects of gravity are becoming negligible and a new constant of motion appears (the angular momentum). In both limits, the additional constant of motion forces the phases curves to move on a torus (doughnut) and after a suitable change of coordinates, we obtain a dynamical system similar to the example of two independent circular motions discussed in the first section. In general, the ratios of the periods will be irrational and the motion quasiperiodic. As we have seen in this example, small changes in the initial conditions are not amplified during the evolution of these systems.
On the other hand, in the intermediate energy region, the numerical simulations
show that minute changes in the initial
conditions can have dramatic consequences. In this case,
we use the terminology sensitive dependence on the initial conditions
or chaotic behavior.
More quantitatively, if the distance between two points of the phase space
is d(0) at t=0 and if the distance d(t) between the two points at time
t grows like ![]() , we call
, we call ![]() a Lyapunov exponent. The Lyapunov exponent has a dimension which is the
inverse of a time. They are usually hard to calculate.
An example of calculation of calculation of Lyapunov exponents is presented
by J. Laskar in Nature vol. 338 p. 238 (1989). This author found
a surprisingly large (maximal) Lyapunov exponent
a Lyapunov exponent. The Lyapunov exponent has a dimension which is the
inverse of a time. They are usually hard to calculate.
An example of calculation of calculation of Lyapunov exponents is presented
by J. Laskar in Nature vol. 338 p. 238 (1989). This author found
a surprisingly large (maximal) Lyapunov exponent ![]() .
See also the notes for chapter 10 in Ruelle's book (p.177).
Lyapunov exponent can be calculated more easily for system with discrete time
.
See also the notes for chapter 10 in Ruelle's book (p.177).
Lyapunov exponent can be calculated more easily for system with discrete time