Classical mechanics provides many examples of deterministic evolution with a continuous time. Newton gave us some general principles to find the rule of evolution in particular circumstances.
Newton's first laws asserts that in special frames of reference called inertial frames, if an object is ``left alone'', it either stays at rest or keeps moving with a constant velocity. The velocity is defined as the time derivative of the position, the time derivative of the velocity is called the acceleration. Our ability to identify inertial frames is clearly dependent on our ability to determine when an object is left alone or not. Newton's second law asserts that in inertial frames, the change of velocity is due to forces acting on the object considered. More precisely, the mass of an object times its acceleration is equal to functions of the position and velocity called forces.
We shall not discuss the existence of inertial frames or the methods to determine the mass of an object. We shall simply state that in many examples, one can in good approximation, establish that the state of the system is determined by the positions and velocities and that the rules of evolutions are given by expressing the acceleration in terms of the positions and velocities. We shall discuss a few simple examples: oscillations of a spring, simple pendulum and double pendulum.
One of the simplest example of Newtonian mechanics is an object of mass m
attached at the end of a spring. Let assume that the object can only move
in the vertical direction. We denote the vertical position by x. If the
object is at rest, we say that x=0. If the spring is stretched, x>0.
In order to specify the state of the system, we need to introduce another
variable which takes into account the fact that different velocities
are possible for a given position at a given time. Usually one takes the
momentum 
. 
is the second derivative of x
(called the acceleration) times the mass and
is equal to the force which acts in the
opposite direction to the displacement with respect to the equilibrium
position. If x>0, the spring is stretched and pulls back toward the
equilibrium point. In other words 
where k is a positive
constant depending on the nature of the spring. The ODE can be summarized
as
An important feature of this ODE is that it has a constant of motion called the energy
The phases curves have a constant energy and form concentric ellipses. If we take a system of units where m=1 and k=1, the equations of motion have the same form as the third case studied in the exercises on ODE.
The case of the
planar pendulum (see Fig. 6) is slightly more
complex. Again the mass m and the length l are given for
definiteness and do not play any important role in the rest of the discussion.
The angle 
is expressed in radians where a complete revolution
amounts to a change by 
.
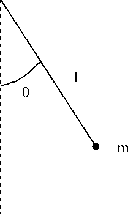
Figure 6: The planar pendulum.
The state of the system is described by the angle and another
variable proportional to the angular velocity which we will
define as 
.
The equations of motion read
where g is the gravitational constant (9.8 meter/second 
).
The constant of motion is
Some phase curves are shown below. One can see that there are two types
of phases curves. The ones for which theta reaches a maximal value and
retraces its way backward (those curves wrap around the center)
and the curves for which keeps increasing indefinitly.
Note that has to be understood modulo 
(even
if it keeps growing on he figure).
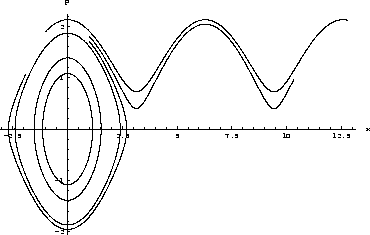
Figure 7: Some phase curves of the planar pendulum.