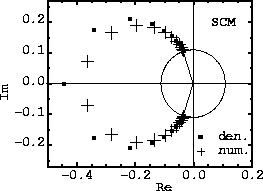
Figure 9: Real and imaginary parts of the roots of the denominator
(filled squares) and numerator (crosses) of
a [26/23] Padé approximant for the critical potential.

Figure 9: Real and imaginary parts of the roots of the denominator
(filled squares) and numerator (crosses) of
a [26/23] Padé approximant for the critical potential.
Work in Progress, Plans: