We have seen in the previous section that the distribution of values
for the quadratic map with a=2 was quite irregular.
We can nevertheless find remarkable regularities in this distribution
if we consider long series of values. in order to study the distribution
of values we proceed as follows. We first display the
successive values of 
(0.4 on the figure), 
etc...
We then divide the values taken by 
into a certain number of
horizontal strips or ``bins'' as
shown in Figure 1 with 10 bins for the first 100 values.
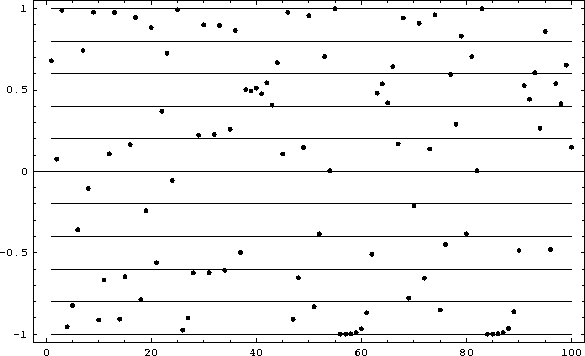
Figure 1:
versus n, 100 iterations of the quadratic map with a=2 and
x(0)=0.4.
Counting the number of
``visits'' in each bin gives us an idea about the values of
which appear more often. For instance in Figure 1, the first
bin represents values between -1 and -0.8 and is visited 21 times, much
more than the fourth bin (values between -0.4 and -0.2) which is visited
only five times. The number of visits for each bin is displayed in
Fig. 2
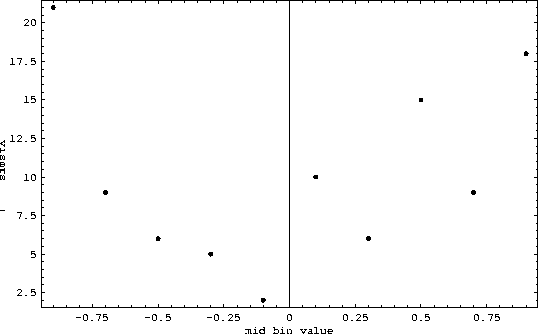
Figure 2: Number of ``visits'' in each bin versus the mid bin value
Since we have only used 100 iterations, large fluctuations (this will be explained later) are observed. A smoother distribution is obtained in the case of 100,000 values in 100 bins as shown in Figure 3.
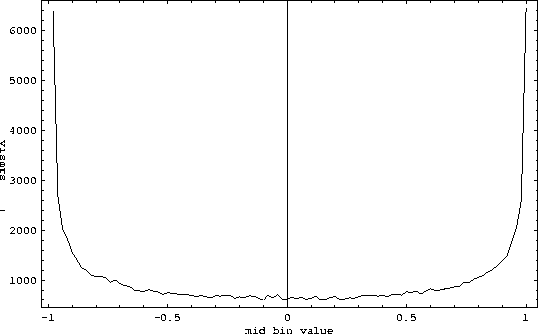
Figure 3: Same as previous figure but with 100,000 values in 100 bins.
The width of the bins is now 0.02. Among the 100,000 values,
we found for instance 689 of them between between -0.42 and -0.40.
Consequently
our estimate for the ``chance'' for to be between -0.42 and -0.40 is
about 689/100,000=0.00689, less than one chance in one hundred.