State of the System: Two points on their respective circle. Using
the same conventions as before, we call these two points x and y,
each of them considered 
.
Rule of Evolution:
Motivations: This rule describes two points in independent uniform
circular motion with respective periods 
and 
.
The evolution of realistic systems like the double
pendulum is more evolved, however the concepts developed in
the simplified case will remain useful.
See also Chapter 10 of Chance and Chaos and especially
the Notes related to this chapter (p.177).
Main Results: The evolution consists in straight
lines of slope 
drawn on a square where the opposite sides are identified (one obtains
some kind
of ``doughnut'' (called torus by mathematicians) this way).
If is rational
the line ends up retracing its former path (periodicity). If
is irrational, the line never retraces exactly its former path
and covers uniformly (after an infinite amount of time) the torus (ergodicity).
In the second case, we often say that the evolution is quasiperiodic.
In order to understand these results, one can first notice that if we
temporarily forget about the instruction, the evolution
consists in straight lines because the change in x is proportional
to the change in y at any time. The instructions amount
to identifying the 
squares which can be used to tile the
x-y plane.
This is illustrated in Fig. 
.
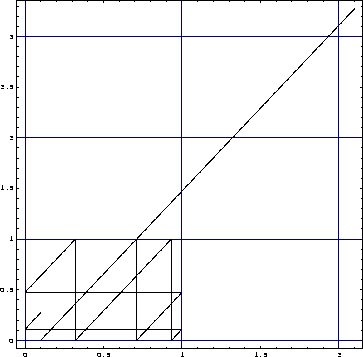
Figure: An example with x(0)=0.1, y(0)=0, 
and 
The conditions
for having periodic or ergodic behavior are very similar to
those found in the previous example.
We can observe the motion of x at stroboscopic times in such
a way that
at each observation y has returned at its initial position. For
instance we can take 
and the successive
positions of x are described as in the previous
example with 
.
If 
is irrational, x will take all the possible values
while y stays at its initial value.
We can then repeat the reasoning starting at slightly larger times and so on,
and
convince ourselves that if is irrational, the entire
square will be covered.
Important Concepts: Quasiperiodicity and the same concepts as in the previous Example .
Exercise : Draw the lines describing the evolution of the system
for 
. Compare your results at
with the results of Exercises of the previous examples.
After how long does the system return to its initial state?
How would your results be affected if you had taken x(0)=0.001
instead of x(0)=0?